NetFork: Mapping Time to Space in Network Visualization

  • Proceedings of the International Working Conference on Advanced Visual Interfaces. ACM 2016

Requirements：

  1. Overview of dynamic activity. 动态活动的概览
  2. Change-cause analysis. 分析变化发生原因
  3. Identification of impacted sources. 分辨出有影响的源
  4. Detailed analysis of the temporal evolution of a source-destination path. 对路径的时序演化进行细化分析

其他不是很有参考价值。

Visualizing a Sequence of a Thousand Graphs (or Even More)

  • EuroVis 2017

文章解决了具有超过 1000 个时间片段的动态图的展示问题。

可视化

  1. 每一个时间步的独立编码：

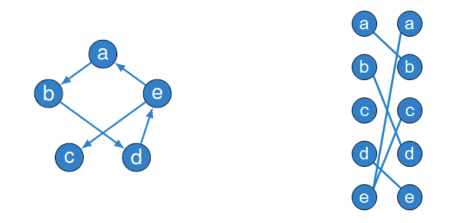
    转换成二部表示，左边的有向图可以被编码成右图的形式，然后利用抛雪球算法（splatting）来减少边相交；

    image-20190109101702184

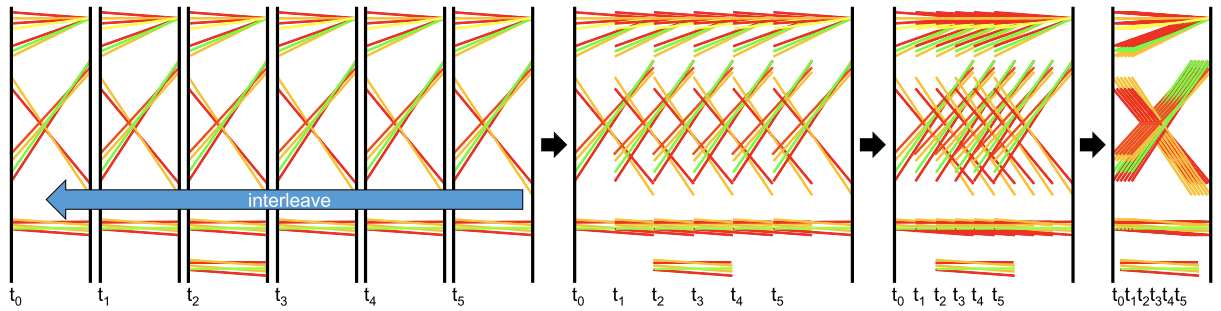
  2. 不同时间步的叠加：

    将不同的时间片叠加在一起，但保留一个像素的偏移，最终产生最右边的结果

    image-20190109104128274

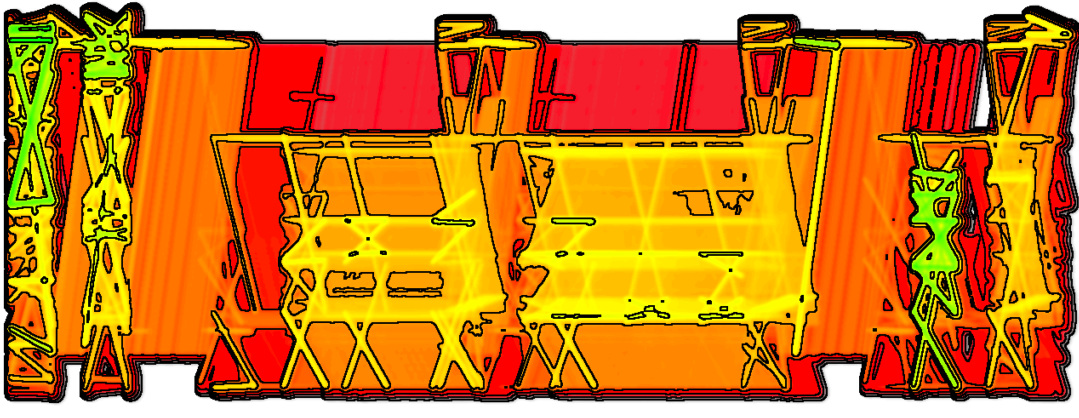
  3. 低通滤波：

    当简单进行叠加时，可能产生下图（a）的结果，边之间有较多的交错；为了使得结果更加平滑，可以使用低通滤波器。不断使用箱型滤波器（box filter）后，就会产生下面（b）（box filter 十次迭代）（c）（box filter 二十次迭代）的结果，边之间的相交更少了，细节变得不可见的同时，一些较大规模的结构也更容易被看到。image-20190109104342835

  4. 每一个时间步的宽度调节

    每一个时间步的宽度较小时，就会变成一条直线；但太大时，屏幕空间要求就会加大，能展示的时间步数量就会下降。

    ​

  5. 等高线：

    假如等高线之后，就能更好的描述可见结构的形状。

    image-20190109110448825

交互

  1. 过滤：多种过滤机制来过滤节点、时间等
  2. 聚合和聚类：对接点进行聚合、聚类等
  3. 细节：corsshair function 来追踪垂直和水平的位置；

Patterns

  1. 一般的 Pattern
  2. 边 Pattern
  3. 动态 Pattern
    • repeating patterns
    • trend patterns
    • contertrend patterns（逆向的）
    • temporal shifts
    • oscillating/alternating patterns
    • outlier/anomaly patterns

Let It Flow: a Static Method for Exploring Dynamic Graphs

  • Visualization Symposium (PacificVis) 2014

用于总结动态图中的结构特征的标准有：degree, betweenness, closeness, cluster coefficient

  1. 根据节点的结构特征（degree, betweenness, closeness, cluster coefficient 等）为每个时间步的节点排序，多个时间步最终组成一个矩阵（图中的节点颜色表示了节点的类别信息）：

    image-20190109141500847

  2. 根据节点排序的上升下降来为每个时刻的每个节点生成向量：

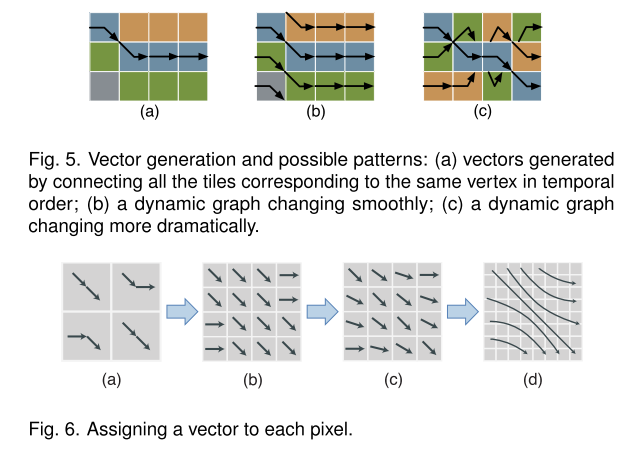
    image-20190109142010096

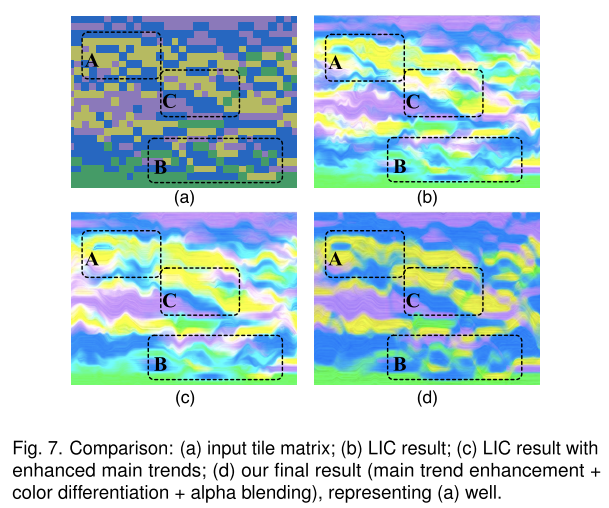
  3. 利用 Line Integral Convolution（LIC）将向量渲染成一系列连续的流图（下图 a 至 b）

  4. 将相似颜色、相似方向的向量进行合并以加强主要的趋势（下图 c）

  5. alpha blending（下图 d）

    image-20190110160848832

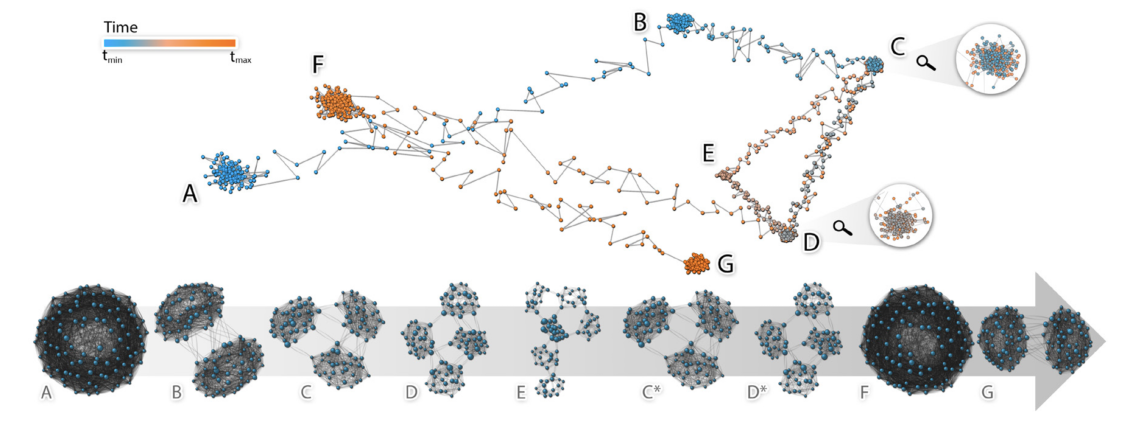
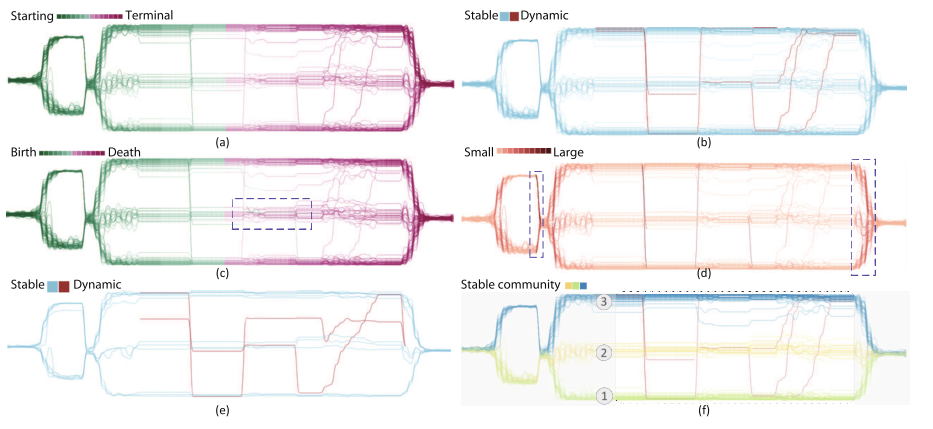
Exploring Evolution of Dynamic Networks via Diachronic Node Embeddings

  • 2018TVCG

五个设计目标：

G1. The evolution analysis of the network as a whole. 网络整体的演变分析

G2. The evolution analysis of dynamic nodes. 动态节点的演变分析

G3. The temporal analysis of temporal communities. 动态社团的时序分析

G4. The structural analysis of stable communities. 稳定社团的结构分析

G5. Relate the analysis to the original networks. 将分析关联至原始网络（可以用来验证）

方法：

  1. 对每一时间步的每一个节点都做了高维空间嵌入（为了保证每一帧的嵌入结果尺度一致，作者做了一个缩放 Embedding Alignment）
  2. 利用 PCA 将至一维，颜色可以用来编码：时间、节点年龄、节点分类、演变值等等
  3. 这个方法的好处在于，图嵌入方法将至一维后仍然能够很好地将社团聚集在一起

image-20190111165723729

Reducing Snapshots to Points

image-20190111203134834

  1. Discretization：将事件离散化为多个动态网络
  2. Vectorization & Normalization：将$|V|\times|V|$的邻接矩阵表达转换为行向量$1 \times |V|^2$，N 个帧就会形成$N \times |V|^2$的矩阵，每一行表达一帧，每一列则是一条边随着时间的变化。当然，除了邻接矩阵，其他矩阵也可使用。对这些高维空间的向量进行归一化，比如：Binarization，Min-Max，Z-score 等。
  3. Dimensionality Reduction：先使用了 PCA，但是也可以使用 MDS 和 t-SNE（这两者在欧几里得距离度量下表现较好）。kolmogorov-smirnov test 和 Degree Distribution Quantification and Comparison 可以用于提供两个网络之间的结构比较（距离计算）

image-20190111204346817